bene : studio is a global consultancy, helping startups, enterprises and HealthTech companies to have better product

Fixed-Point Combinators in JavaScript

February 16, 2017 -

At bene : studio we love knowledge sharing to help the community of professionals. With 10+ years and over 100 projects behind us, we have a vast amount of experience. This is why we have launched a knowledge base on our blog with regular updates of tutorials, best practices, and open source solutions.

These materials come from our internal workshops with our team of developers and engineers.

Pardon the interruption, we have an important message!

We are looking to expand our team with talented developers. Check out our open positions and apply.

An introduction to fixed-point combinators and lambda calculus with real-world JavaScript examples showing their power and beauty.

TL;DR

Lambda calculus can give you a deeper level of understanding of how functions work and how they relate.
Fixed-point combinators can help you to implement recursion.
Learning new stuff makes you stronger and better as a software engineer.
Scroll to the bottom for practical applications.

Fixed-Point Combinators

Fixed-point combinators are higher-order functions such that:

y f = f (y f)

for all f where y is a combinator, f is function and space is function application. This expands as follows:

y f = f (y f)
    = f (f (y f))
    = f (f (f (y f)))
    = ...

This expansion is recursion.

With the use of combinators we can define self-referencing anonymous functions avoiding the use of variables. Let’s see the most simple one!

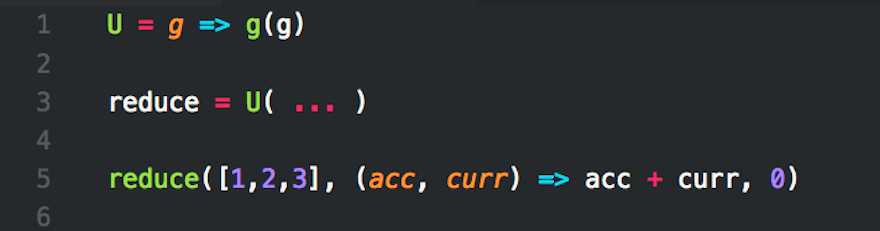
The U Combinator

The U combinator is the most simple fixed-point combinator.

U g := g gU = λg.(g g)

where λg. is lambda abstraction, which is the definition of an anonymous function that takes an argument g and substitutes it into its expression.

Example in JavaScript

Define the U combinator in JavaScript ES6 with arrow function.

U = g => g(g)

In practice we want our recursions to halt so we can calculate something. With currying we can introduce a halting condition.

Let’s calculate factorial with the U combinator.

fact = U(
  g => // g for self-referencing
    x => // currying is for passing the halting condition
      (x === 0) // halting condition
        ? 1 // halt
        : x * g(g)(x - 1) // recursion
)fact(5) === 120 // true

The Y Combinator

The Y Combinator in Lambda Calculus

Haskell B. Curry defined the Y combinator as follows.

Y := λf.(λx.f (x x)) (λx.f (x x))

The Y combinator could be used even in this form but we can simplify it.

Lets do β-reduction.

Y g := (λf.(λx.f (x x)) (λx.f (x x))) g
     = (λx.g (x x)) (λx.g (x x))
     = g ((λx.g (x x)) (λx.g (x x)))
     = g (Y g)

The reduced form reveals that this is a fixed point combinator:

Y g = g (Y g)Y = λg.(g (Y g))

The Y Combinator in JavaScript

The Y combinator works only in lazy languages such as Haskell. In non-lazy languages like JavaScript the intuitive implementation expands until stack overflow or never halts in case of tail call optimization.

Y = g => g(Y(g)) // intuitive implementation
Y( a => a ) // call the Y combinator with the unit function
Uncaught RangeError: Maximum call stack size exceeded

Solution: let’s define laziness in JavaScript: wrap Y(g) in a zero-arity function.

Y =
    g => g( () => Y(g) )

This way we can avoid automatic expansion. Let’s calculate factorial with Y.

fact = Y(
  g => // g for self-referencing
    x => // this curryed function is returned by g()
      (x === 0) // halting condition
        ? 1 // halt
        : x * g()(x - 1) // recursion
)fact(5) === 120 // true

The difference to the previous implementation is that there is no need to pass g to g(), it is already bound.

The Z Combinator

The Z Combinator in Lambda Calculus

Z := λg.(λx.g (λv.((x x) v))) (λx.g (λv.((x x) v)))

There is an extra v argument and an extra function application which is not present in the case of Y combinator definition.

After β-reduction we got:

Z g v = g (Z g) vZ g = λ.v(g (Z g) v)Z = λv.(λg.(g (Z g) v))

The Z Combinator in JavaScript

An extra v parameter and function application to the Y combinator gives us the Z combinator.

Because of the extra parameter v we do not need to construct a lazy recursion in JavaScript.

Z =
    g => v => g(Z(g))(v)

Let’s define a function that sums up the numbers from a given whole number to an other one.

example series: 5 6 7 8
sum: 26

Define the sum function with the Z combinator:

// sum(from, to)
sum = Z(
  g => // g for self-referencing
    from =>
      to =>
        (from === to) // halting condition
          ? to // halt
          : from + g(from + 1)(to) // step one and recurse
)sum(5)(8) === 26 // true

We can see that there is no extra laziness implemented because the function application is lazy in itself.

The Connection Between U, Y and Z

Let us consider the JavaScript implementations.

U = g => g(g) // recursion is strict, must curry
Y = g => g( () => Y(g) ) // we made the recursion 'lazy'
Z = g => v => g(Z(g))(v) // explicit currying makes it 'lazy'

Practical Examples in JavaScript

Here are some real-world examples using fixed point combinators.

Accept Terms

We would like users to accept terms. Ask them until they accept it.

It can be done without naming a function for the recursion.

Y(ask =>
  (prompt('Accept terms?') !== 'yes')
    ? ask()
    : alert('Thanks!')
)

We can even count how many times a user did not accept terms.

Y(ask => count =>
  (prompt('Accept terms?') !== 'yes')
    ? ask()(count + 1)
    : alert('At last! It took ' + count + ' times.')
)(1)

We can notice that counting is done via currying.

You can read more on Currying in JavaScript ES6.

Fetch Retry

We can retry unsuccessful fetch() or XHR operations with a maximum number of attempts with manual operation on the UI.

Y(
  retry =>
    attempts =>
      fetch('/betcha-cant-load-this')
      .then(
        res => res.ok
          ? alert('Loaded!')
          : (
              (attempts > 1 && confirm('Reload?')) // retry on UI
                ? retry()(attempts - 1)
                : alert('Could not load. ' + res.status)
            )
      )
)(5)

Conclusion

I believe that lambda calculus and functional programming can help software engineers organize their thoughts in a consistent and rigorous way that helps write good quality code.

Enjoy the world of combinators and functional JavaScript.